Using the lowest possible amount of bots in the network, while maintaining full production, results in the best performance.
In this test we try and find out if there is a performance penalty for having too many or too few logistic bots in a bot network, and if there is, find out the ideal amount.
For this test, we set up a bot build that is rotationally symmetrical to ensure efficient bot travel, while still having a reasonably high count of active bots (around 300). The build produces iron chests from iron ore. Furthermore, recipes are clocked in a way that each quadrant outputs with its own offset, to ensure that bot usage remains as constant as possible throughout the runs.
Next, we set up the build with the lowest amount of bots possible that ensures full production sustained for a long period of time (1h). Through trial and error, this number resulted in 403 total bots.
At this minimum number of bots, it appears that the full 403 bots get used. But as bots are additionally added, the apparent number of active bots in use decreases. By measuring the number of active bots in a cell with a large bot excess, the number of bots in use appears to be ~310. (Blueprint)
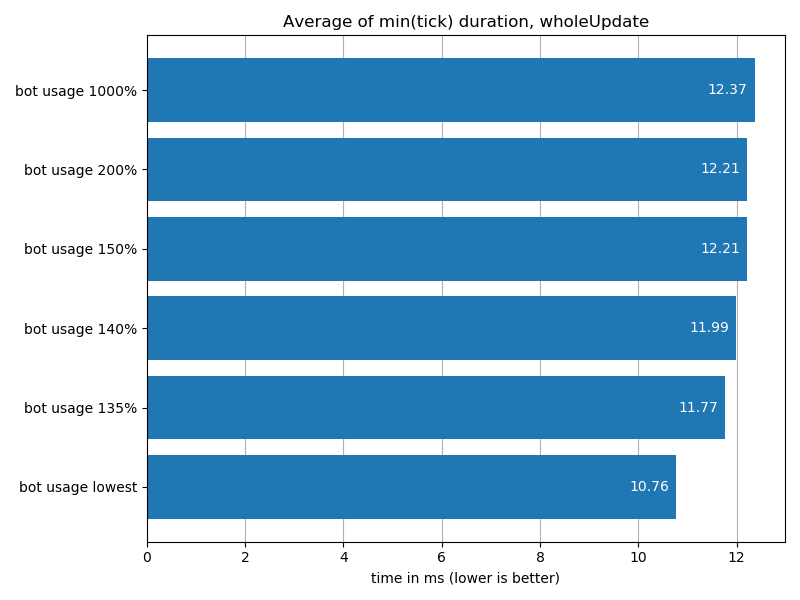
Using this ~310 number as the baseline, the lowest number of bots effectively becomes a factor of 130%. Continuing with linear percentage increases, we also test (130%), 135%, 140%, 150%, 200% and 1000% of that 310 number. These percentages correspond to bot networks with logistic bot counts of (403), 418, 434, 465, 610, and 3100 respectively.
Benchmarks were conducted using the inbuilt Factorio benchmarking utility. Each map was benchmarked 30 times, for 720 ticks each.

The data paints a clear picture: each increment of bots on top of the lowest possible amount results in a degradation of performance. Most notably, the biggest difference between two consecutive saves is the one between the lowest possible, and its neighbor with just a 30 bot increment.
If we simply look at the amount of active bots in each save, these results seem counterintuitive since the save with the lowest amount of bots in the network has the highest amount of active bots, while the save with the most bots in the network (1000%) has the lowest amount of active bots.
To further analyze these results, we do a sleepy profile on the saves with the lowest amount of bots in the network and the save with 150% bots relative to the normal amount of active bots. The results were the following:
| Function | lowest | 150% |
|---|---|---|
| logisticNetwork::findBestAvailableRobot | 1.02s | 3.61s |
| logisticCell::spawnRobot | 0.05s | 0.53s |
| logisticNetwork::fillRequesters | 2.85s | 5.35s |
| logisticRobot::update | 4.29s | 3.86s |
| logisticRobot::moveToStationingLogic | 0.49s | 2.27s |
The function logisticRobot::moveToStationingLogic is responsible for the process of bots docking, entering a roboport and becoming idle. Usage here is minimal in lowest because bots in this save tend not to dock, they instead recharge and continue fulfilling jobs.
The biggest difference lies in logisticNetwork::findBestAvailableRobot. Examining its child call logisticCell::spawnRobot, we learn that the cost of de-spawning and spawning bots is significant. On top of that, we see from logisticNetwork::fillRequesters that when looking for a bot to fulfill a request it is significantly faster to pick one that is already in the air than it is to look through the roboports and find an idle bot.
Lastly, logisticRobot::update confirms that the save with the lowest possible amount of bots has the highest amount of active bots, but this higher cost is completely offset by the cost of repetitive spawning and de-spawning bots (docking).
On a logistic bot network, reducing the amount of bots to the point where they avoid docking, but still maintaining full production results in the best performance.